PROBLEM 23

(ALG/CH)

PROBLEM 22: FIND THE LOCUS OF THE POINT.

If the sum of the distance of a point from the two perpendicular lines in a plane is 1, then find the locus of the point. (COR/M)

PROBLEM 21: FIND THE RATIO

A straight line through the origin O meets the parallel lines 4x + 2y = 9 and 2x + y + 6 = 0 at points P and Q respectively. Find the ratio in which the point O divides the segment PQ . (COR/CH)

SOLUTION OF PROBLEM: 18

(IC/M)

SOLUTION OF PROBLEM: 17

(IC/M)

Problem 20 : SLOPE OF THE TANGENT

(COR/M)

Problem 19 : Order of the differential equation

Find the order of the differential equation of all parabola with axis parallel to the axis of y. ( DC/M)

SOLUTION OF PROBLEM: 16

(ALG/E)

SOLUTION OF PROBLEM: 15

(V&3D) 

Problem 18: Solve the differential equation

(IC/M)

Problem 17: Determine the vaue of n.

(IC/M)

MATHSIIT WISHES U A VERY PROSPEROUS DIWALI

      MATHSIIT WISHES YOU A VERY

               HAPPY & PROSPEROUS

                      DIWALI

CONDITION OF LINE BEING NORMAL TO ELLIPSE

What is the condition for line y = mx + c to normal a standard ellipse ? (asked by VANI RAVIJA)

PROBLEM 16: FIND THE VALUE a+b+c+d

(ALG/E) 

PROBLEM: 15 WHICH OF THE EXPRESSION EXISTS

( V&3D/E)

SOLUTION OF PROBLEM: 14

(IC/M)

SOLUTION OF PROBLEM: 13

(DC/CH) 

SOLUTION OF PROBLEM: 12

Find the values of a, b, c and d for the given limit.  (DC/M)
SOLUTION:

SOLUTION OF PROBLEM: 11

Plot the curve of y = |tan(x)|   (DC/M)
SOLUTION : We already know how to plot the curve of tan(x). |tanx| will always yield positive values, which means wherever tan(x) is negative we have to make it positive in order get |tan(x)|  curve.

Therefore we have to invert the negative strip of tan(x) curve.

IIT PROBLEMS ON VIDEOS

PROBLEM: 14 FIND THE VALUE OF DEFINITE INTEGRAL

                                                                                             (IC/M)

PROBLEM 13: FIND THE VALUE OF LIMIT

                                                                                           (DC/CH)

SOLUTION OF PROBLEM: 10

Let function f is from R to R be defined by f(x) =2x + sin(x) for x belongs to R. Then f is

a) one-to-one and onto

b) one-to-one but not onto.

c) onto but not one-to-one

d) neither one-to-one nor onto.      ( DC/CH)

SOLUTION: The given function has co-domain as R( set of all real numbers)

For the function f(x) = 2x + sin(x) , 2x ranges from negative infinity to positive infinity whereas sin(x) varies from [-1,1] so ultimately the f(x) will have its range as R. Therefore, the f(x) is Onto function.

Also, f'(x) = 2 + cos(x) , cos(x) will vary from [-1,1], So 2+cos(x) varies from [1,3].

Therefore, f'(x) is always positive. Hence f(x) will always be an increasing function.Therefore, f(x) will be one-to-one.

So, the correct option is (a)

SOLUTION OF PROBLEM: 9

Find the area bounded by the curve y = e(x) and the lines x = 0 and y = e. ( IC/E)
SOLUTION: 

NOTE: e(x) is e to the power x

SOLUTION OF PROBLEM: 8

Prove that the f(x) = 2(x)cube + 3(x)sq+6x +10 will always be an increasing function. (DC/M)

Solution: If we differentiate the given function we will get f'(x) = 6(x)sq + 6x +6 = 6( (x)sq +x +1)

Now, we can write f'(x) = 6[(x + 1/2)sq +3/4] which is always positive.So f(x) will always be an increasing function.

Alternatively, we can also say the for the quadratic expression (x)sq +x +1 coefficient of (x)sq is positive and discriminant is negative (-3), so the expression is always positive

SOLUTION OF PROBLEM: 7

Let z and w are two non-zero compex numbers such that |z| =|w| and arg(z) + arg(w)=180(degree), then z is

SOLUTION: we can have two different ways to approach the solutions

CONVENTIONAL METHOD: 

Let z = r e(ip) , where r is |z| and p is arg(z)

also, w = r e(iq), where r is |w| and q is ar(w)

as given |z|=|w| and p + q =180(degree), we can write w = r e(i(180-p))= r(cos(180-p)+i sin(180-p))

w = r(-cos(p) +i sin(p)) = -r( cos(p) - isin(p)) = -1/z =-z( bar).

Hence, w = -z(bar)

NOTE: e(ip) is e to the power ip.

GRAPHICAL METHOD:

SOLUTION OF PROBLEM: 6

Find the value of k such that x +y = k is normal to the parabola (y)sq =12x. (COR/M)

SOLUTION: We already know that y = mx -2am -a(m(cube)) is normal to the parabola y(sq)=4ax. Here in the given problem a=3 and if we compare x +y = k with the standard equation of the normal we get m=-1 and k = -2am -a(m(cube)).

By putting the values of m and a, we get k =9

NOTE: y(sq) is y square and m(cube) is m cube

POST UR PROBLEMS

YOU CAN POST UR MATHS PROBLEMS BY JUST SIGNING IN WITH YOUR GMAIL OR YAHOO MAIL ID, AND POST UR PROBLEMS IN  GET ANSWERS SECTION.

                         

                                                                                                       

GRAPH OF ONE-TO-ONE FUNCTION

UR QUESTIONS, OUR SOLUTION: 3

How a one-to-one function looks like on cartesian plane ? ( DC/M)
( asked by RAVI JHA)

SOLUTION: One-to-one functions has unique mapping, that is for a unique value of x we will have unique value of y. All functions which are strictly increasing or strictly decreasing in their domain will be one-one functions.

Otherwise, they will be many-one.

For eg: y = x, y = log(x), y = e(x) are all strictly increasing function they will be one-to-one.

y = -x , y =e(-x) are strictly decreasing functions they will also be one-to-one.

whereas, y= sin(x) , y = |x|, y = x(sq), y= cos(x), y = tan(x) will all be many-one functions because their graph is decreasing for some values of x and increasing for others.

Note: e(x) is e raise to x, e(-x) is e raise to -x, x(sq) is x sqaure

FIND THE VALUES OF a, b, c and d

PROBLEM : 12

Find the values of a, b, c and d such that   ( DC/M)

     


     

MEET THE TOPPER

GRAPH OF |tanx|

PROBLEM: 11

Plot the curve given by the function y = |tanx|  (DC/M)

SOLUTION OF PROBLEM: 5

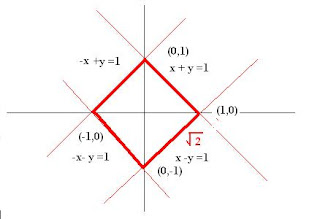
Find the area enclosed by the curve |x| +|y| =1 (IC/M)

SOLUTION: The equation will have four different cases

x + y =1, when x>0 and y>0 ( we will draw x + y=1line & will take its part which is lying in Ist quadrant)

 x-y =1, when x>0 and y<0 ( we will draw x - y=1line & will take its part which is lying in IVth quadrant)

-x +y =1,when x<0 and y>0 ( we will draw -x + y=1line & will take its part which is lying in IInd quadrant)

-x -y =1,when x<0 and y<0 ( we will draw -x - y=1line & will take its part which is lying in IIIrd quadrant)

The enclosed figure will be a square of a side root(2).

Therefore, the area enclose will that of square that is 2 sq units

SOLUTION OF PROBLEM: 4

Find out the quadratic equation having equal and opposite roots as that of equation (x sq -16) =0.                    ( ALG/E)

.
 Note: (x) sq stands for x square

SOLUTION: The given(x)sq-16=0 has its roots as +4 and-4. According to the given condition the required equation has its roots as equal and opposite to the given equation's roots that is the required equation will have its roots  as -4 and +4 .The required equation will therefore be (x+4)(x-4)=0 or (x)sq-16=0, which is nothing but the original equation. 

ONTO AND INTO FUNCTIONS

PROBLEM: 10

Let function f is from R to R be defined by f(x) =2x + sin(x) for x belongs to R. Then f is

a) one-to-one and onto

b) one-to-one but not onto.

c) onto but not one-to-one

d) neither one-to-one nor onto.      ( DC/CH)

AREA UNDER THE CURVE

PROBLEM : 9

Find the area of the region bounded by the curves y=e(x) and the lines x=0 and y=e . (IC/E)
NOTE: e(x) is e to the power x.

INCREASING FUNCTION

PROBLEM: 8

Prove that the f(x) = 2(x)cube +3(x)square +6x +10 will always be an increasing function. (DC/M)

IIT-JEE 2010 NOTIFICATION

 IIT-JEE EXAM ON 10 APRIL 2010, FORMS WILL BE OUT IN 3RD WEEK OF NOV.

CLICK ON:
http://www.thehindubusinessline.com/blnus/14231455.htm

MAXIMUM DISTANCE OF A LINE FROM A POINT

UR QUESTIONS, OUR SOLUTION: 2

Find the equation of a line passing through (1,2) and having maximum distance from the point (3,1). (COR/M)

( asked by ESHA PRASHAR)

SOL: 

We can solve this problem in two different ways one is using Graphs and other by Conventional method.

GRAPHICAL METHOD

we already know we will have infinetly many lines passing through (1,2), so let's examine all those lines and picked the one having maximum distance from point (3,1).Clearly the line perpendicular to line joining (1,2) and (3,1) is the required line having maximum distance from (3,1).( shown by bold line).

Therefore,the slope of the required line is -(3-1)/(1-2)=2. Hence the line will be (y-2)=2 (x-1) or y=2x.

CONVENTIONAL METHOD

The general equation of line passing through (1,2) is y=mx+2-m. Its distance from (3,1) will be

d=|2m+1|/sqrt(msq+1) where sqrt is square root and m sq is m square.

differentiating d with respect to m, we will get m=2 as the point of maxima.

Therefore, the required will be y=2x.

ARGUMENT OF z

PROBLEM: 7

Let z and w be two non- zero complex numbers such 

that |z|=|w| and arg(z) +arg(w) =180(degree), then z is

                                                                                 (ALG/M)

NORMAL TO PARABOLA

PROBLEM: 6

Find the value of k such that the line x +y =k is normal to the 

 parabola (y)sq=12x.  (COR/M)

NOTE: (y)sq stands for y square.

AREA UNDER THE CURVES

PROBLEM: 5

 Find the area enclosed by the curve |x| +|y|=1 
( IC/M)

OUR SOLUTION OF PROBLEM: 3

Find out the distance between the parallel lines given by x + 3y =7 and 5x + 15y = 25. ( COR/E)

Solution: We already know the formula to get the distance between two parallele lines.

ax +by+c=0 and ax+by+d=0 are parallel lines , the distance between them is |c-d|/sqrt( asq +bsq)

where sqrt stands for square root and sq stands for square.

 lines x + 3y =7 and 5x + 15y = 25 are || but the coefficient of x and y of both the equation are not equal.

So, let's make them equal by dividing 2nd equation by 5

We have  x + 3y -7=0 and   x + 3y -5=0 by applying the above formula

distance=|5-7|/sqrt(10)= 2/sqrt(10)

OUR SOLUTION OF PROBLEM: 2

Find the interval in which 
f(x)=2log(x-2)-xsq+4x+1 increases
a) (1,2)
b) (2,3)
c) (5/2,3)
d) (2,4)

Note: xsq term stands for x square.                         (DC/M)

SOLUTION:

Before starting up the problem, let’s first of all find out the domain of the given function

Since, we have (x-2) is inside the log it should be positive, it will happen only when x>2.

Hence the domain of given function is x > 2 therefore option a) is ruled out.

Now differentiate the given function, we get f ‘(x)= -(x-3)(x-1)/ (x-2)

For f(x) to increasing, f ‘ (x) > 0

Since, x> 2, the denominator of f ‘ (x ) is always positive, which means for f (x) to increasing -(x-3)(x-1) >0

which means x will lie from ( 1,3), but since the function is defined for x >2, we will have (2,3 )as the interval where function is increasing.

Hence the correct choices are (2,3) and (2.5 ,3)

 

GRAPHS OF |sinx| and (sinx) square

UR QUES, OUR SOL: 1

Q. What is the difference between the curves of |sinx| and (sinx) sq.    ( DC/ M)

(asked by RAVI JHA)

SOL: The curve of y = |sinx| can easily be drawn from the sinx as the portion of the curve below x- axis will get inverted.

For the y =(sinx) sq, we can write it as (1-cos(2x))/ 2 , which we can easily plot by plotting cos2x, then inverting and halving it so as to get -cos2x/2 and later shifting the origin, we will get the shape of   

y= (sinx) sq

EQUAL AND OPPOSITE ROOTS

PROBLEM: 4

Find out the quadratic equation having equal and opposite roots as that of equation (x sq -16) =0.       ( ALG/E)

Note: xsq stands for x square.

DISTANCE BETWEEN PARALLEL LINES

PROBLEM: 3

Find out the distance between the parallel lines given by x + 3y =7 and 5x + 15y = 25.   ( COR/E)

OUR SOLUTION OF PROBLEM: 1

QUESTION : Find the equation of the circle touching the axes and having radius of 1 unit.

SOLUTION:

Since the required circle is touching both the axes, the coordinate of the centre of circle will be in the form of (r,r) where r is the radius of circle.
So the eq. of circle will be (x-r)sq +(y-r)sq = r sq
but here we can have in total 4 such circles
Having centre at (+-r, +-r)

Each of these circle will be 4 different quadrant.
In the given problem r=1
So the eq of circles will be
(x-1)sq +(y-1)sq = r sq Ist quadrant circle
(x+1)sq +(y-1)sq = r sq IInd quadrant circle
(x+1)sq +(y+1)sq = r sq IIird quadrant circle
(x-1)sq +(y+1)sq = r sq IVth quadrant circle

DIFFERENTIAL CALCULUS

PROBLEM: 2

Find the interval in which f(x)=2log(x-2)-xsq+4x+1 increases
a) (1,2)
b) (2,3)
c) (5/2,3)
d) (2,4)                                                   ( DC/M)


Note: xsq term stands for x square.

CIRCLE TOUCHING AXES

PROBLEM: 1

Find the equation of the circle touching the axes and having radius of 1 unit.   ( COR/M)

MATHS IIT BLOG IS LIVE !

The much awaited IIT MATHS blog is live now for the IIT-JEE aspirants.
This blog is the collective endeavor of our core team headed by Mr Nishu Kumar Govil.
We seek ur active contribution and participation for this blog.
njoy Maths &; Keep blogging !